Why Backtesting is Not Enough

Overfitting can be especially problematic when we rely solely on backtesting for validation. To improve model performance and interpretation, one must look beyond simple backtesting and consider other analyses like feature importance.

The Importance of Features

Features are the variables or columns in our data that the machine learning algorithm uses for making predictions. Knowing which features are important can help in both understanding how the model is making predictions and in improving the model's performance. This brings us to the subject of feature importance methods.

Dealing with Substitution Effects

In machine learning, a "substitution effect" can dilute the importance of features that are interchangeable. This is similar to "multi-collinearity" in statistics. One way to handle this is to perform Principal Component Analysis (PCA) before feature significance analysis.

Methods of Feature Importance

Mean Decrease Impurity (MDI): This is mainly used in tree-based classifiers. It calculates how much each feature decreases impurity.
- Pros: Quick to compute, well-suited for tree-based classifiers.
- Cons: Susceptible to substitution effects, not generalizable to non-tree-based classifiers.
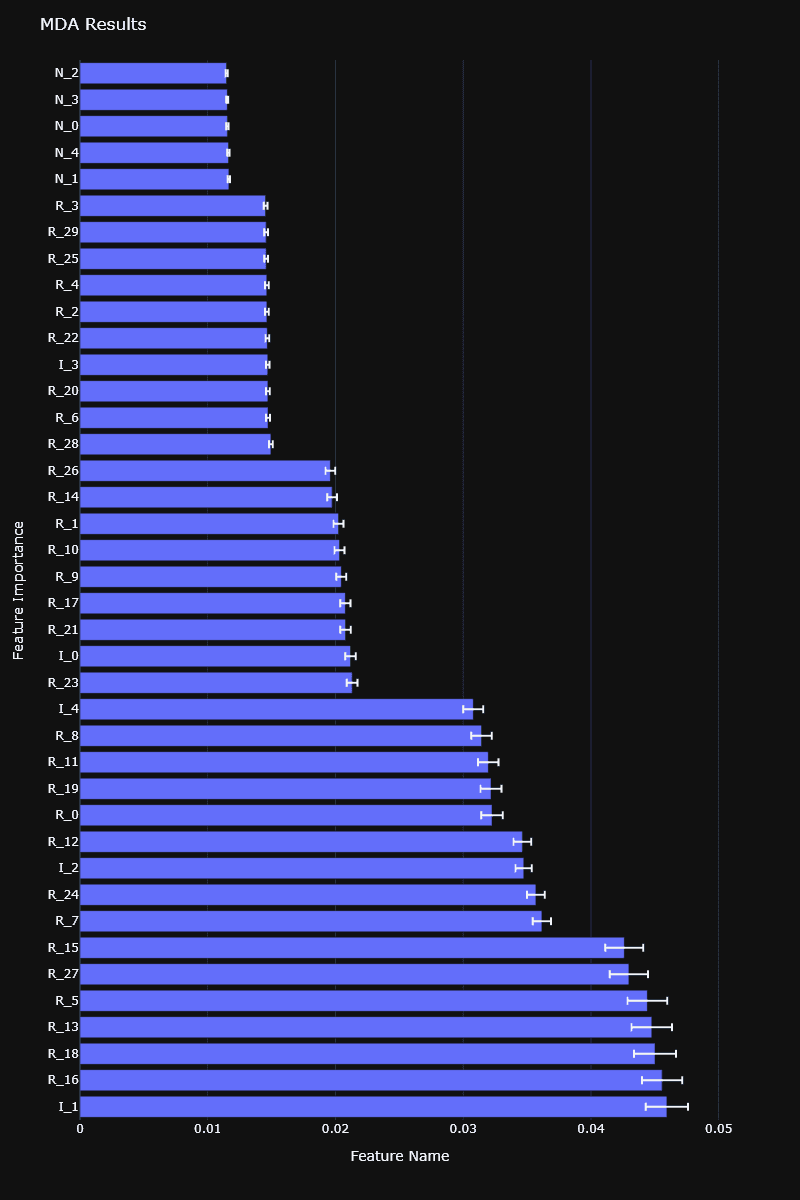
Mean Decrease Accuracy (MDA): This is a more universal method that can be applied to any classifier. It calculates how much the performance decreases when each feature is altered.
- Pros: Applicable to any classifier.
- Cons: Computationally expensive, susceptible to substitution effects.

MDI feature importance computed on a synthetic dataset

Both MDI and MDA feature importances are available in the RiskLabAI library, for both Python and Julia.

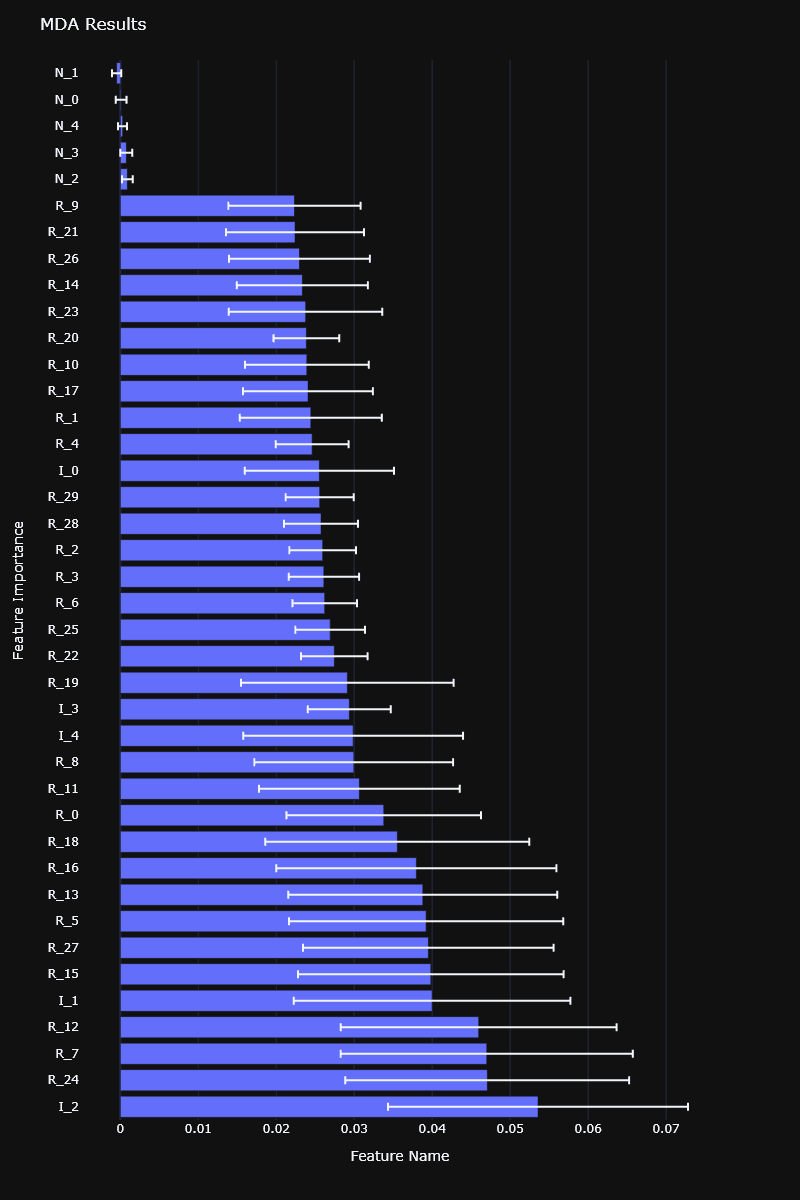
MDA feature importance computed on a synthetic dataset

Here are the implementations for the MDA and MDI feature importance calculations.

feature_importance_mda.py

from RiskLabAI.features.feature_importance.feature_importance_strategy import FeatureImportanceStrategy
import numpy as np
import pandas as pd
from sklearn.metrics import log_loss
from sklearn.model_selection import KFold
from typing import List, Optional

class FeatureImportanceMDA(FeatureImportanceStrategy):
    def __init__(
            self,
            classifier: object,
            x: pd.DataFrame,
            y: pd.Series,
            n_splits: int = 10,
            score_sample_weights: Optional[List[float]] = None,
            train_sample_weights: Optional[List[float]] = None
    ) -> None:
        self.classifier = classifier
        self.x = x
        self.y = y
        self.n_splits = n_splits
        self.score_sample_weights = score_sample_weights
        self.train_sample_weights = train_sample_weights

    def compute(self) -> pd.DataFrame:
        if self.train_sample_weights is None:
            self.train_sample_weights = np.ones(self.x.shape[0])
        if self.score_sample_weights is None:
            self.score_sample_weights = np.ones(self.x.shape[0])

        cv_generator = KFold(n_splits=self.n_splits)
        initial_scores, shuffled_scores = pd.Series(dtype=float), pd.DataFrame(columns=self.x.columns)

        for i, (train, test) in enumerate(cv_generator.split(self.x)):
            print(f"Fold {i} start ...")

            x_train, y_train, weights_train = self.x.iloc[train, :], self.y.iloc[train], self.train_sample_weights[train]
            x_test, y_test, weights_test = self.x.iloc[test, :], self.y.iloc[test], self.score_sample_weights[test]

            fitted_classifier = self.classifier.fit(X=x_train, y=y_train, sample_weight=weights_train)
            prediction_probability = fitted_classifier.predict_proba(x_test)

            initial_scores.loc[i] = -log_loss(
                y_test,
                prediction_probability,
                labels=self.classifier.classes_,
                sample_weight=weights_test
            )

            for feature in self.x.columns:
                x_test_shuffled = x_test.copy(deep=True)
                np.random.shuffle(x_test_shuffled[feature].values)
                shuffled_proba = fitted_classifier.predict_proba(x_test_shuffled)
                shuffled_scores.loc[i, feature] = -log_loss(y_test, shuffled_proba, labels=self.classifier.classes_)

        importances = (-1 * shuffled_scores).add(initial_scores, axis=0)
        importances /= (-1 * shuffled_scores)

        importances = pd.concat({
            "Mean": importances.mean(),
            "StandardDeviation": importances.std() * importances.shape[0]**-0.5
        }, axis=1)

        return importances

View More: Julia | Python

feature_importance_mdi.py

from RiskLabAI.features.feature_importance.feature_importance_strategy import FeatureImportanceStrategy
import pandas as pd
import numpy as np
from typing import List, Optional, Union


class FeatureImportanceMDI(FeatureImportanceStrategy):
    def __init__(
            self,
            classifier: object,
            x: pd.DataFrame,
            y: Union[pd.Series, List[Optional[float]]]
    ) -> None:
        self.classifier = classifier
        classifier.fit(x, y)

    def compute(self) -> pd.DataFrame:
        feature_importances_dict = {i: tree.feature_importances_ for i, tree in enumerate(self.classifier.estimators_)}
        feature_importances_df = pd.DataFrame.from_dict(feature_importances_dict, orient="index")
        feature_importances_df.columns = self.classifier.feature_names_in_

        # Replace 0 with NaN to avoid inaccuracies in calculations
        feature_importances_df.replace(0, np.nan, inplace=True)  

        importances = pd.concat({
            "Mean": feature_importances_df.mean(),
            "StandardDeviation": feature_importances_df.std() * (feature_importances_df.shape[0] ** -0.5)
        }, axis=1)

        # Normalize importances to sum up to 1
        importances /= importances["Mean"].sum()

        return importances

View More: Julia | Python

Understanding Feature Importance with SFI and Orthogonal Features

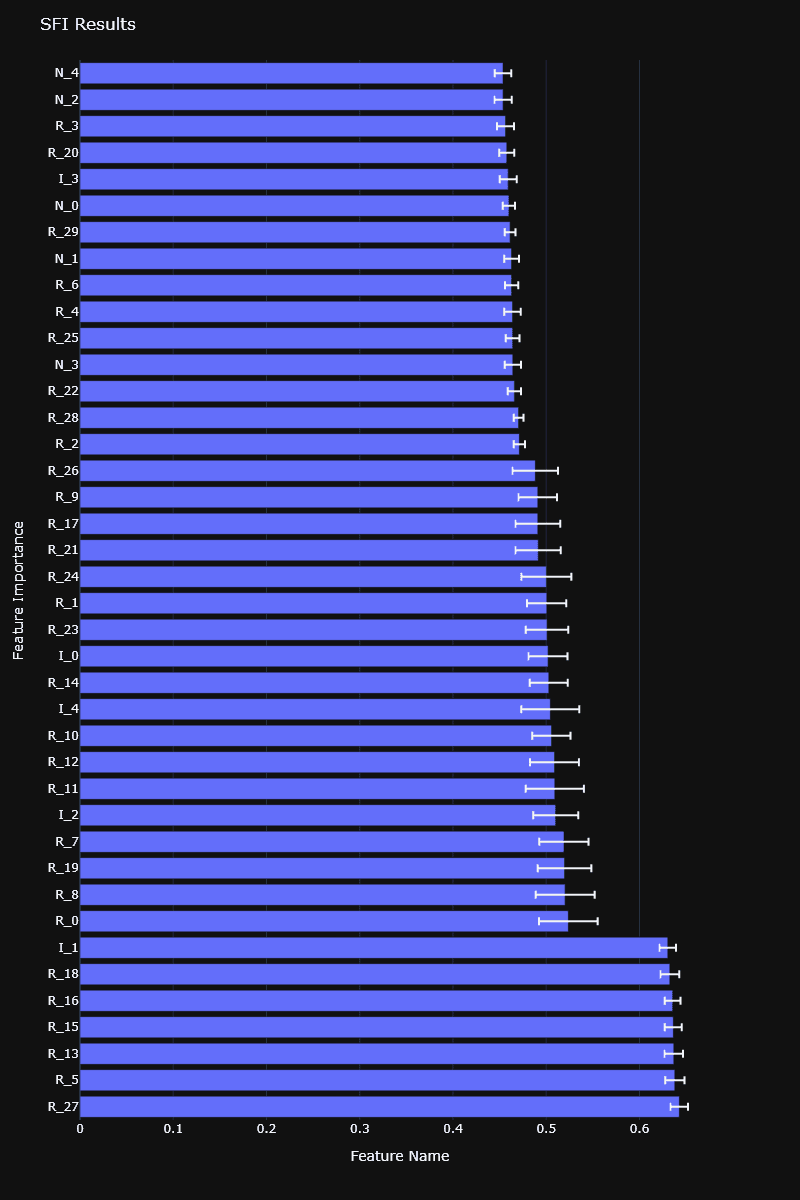
Single Feature Importance (SFI)

Single Feature Importance (SFI) evaluates the out-of-sample (OOS) performance score for each feature individually. It's useful for avoiding the substitution effects that might occur in other methods like MDI and MDA.

feature_importance_sfi.py

from RiskLabAI.features.feature_importance.feature_importance_strategy import FeatureImportanceStrategy
import pandas as pd
import numpy as np
from sklearn.metrics import log_loss, accuracy_score
from sklearn.model_selection import KFold
from typing import List, Optional, Union


class FeatureImportanceSFI(FeatureImportanceStrategy):
    def __init__(
            self,
            classifier: object,
            x: pd.DataFrame,
            y: Union[pd.Series, List[Optional[float]]],
            n_splits: int = 10,
            score_sample_weights: Optional[List[float]] = None,
            train_sample_weights: Optional[List[float]] = None,
            scoring: str = "log_loss"
    ) -> None:
        self.classifier = classifier
        self.features = x
        self.labels = y
        self.n_splits = n_splits
        self.score_sample_weights = score_sample_weights
        self.train_sample_weights = train_sample_weights
        self.scoring = scoring

    def compute(self) -> pd.DataFrame:
        if self.train_sample_weights is None:
            self.train_sample_weights = np.ones(self.features.shape[0])
        if self.score_sample_weights is None:
            self.score_sample_weights = np.ones(self.features.shape[0])

        cv_generator = KFold(n_splits=self.n_splits)
        feature_names = self.features.columns
        importances = []

        for feature_name in feature_names:
            scores = []

            for train, test in cv_generator.split(self.features):
                feature_train, label_train, sample_weights_train = (
                    self.features.loc[train, [feature_name]],
                    self.labels.iloc[train],
                    self.train_sample_weights[train],
                )

                feature_test, label_test, sample_weights_test = (
                    self.features.loc[test, [feature_name]],
                    self.labels.iloc[test],
                    self.score_sample_weights[test],
                )

                self.classifier.fit(feature_train, label_train, sample_weight=sample_weights_train)

                if self.scoring == "log_loss":
                    prediction_probability = self.classifier.predict_proba(feature_test)
                    score = -log_loss(
                        label_test,
                        prediction_probability,
                        sample_weight=sample_weights_test,
                        labels=self.classifier.classes_,
                    )
                elif self.scoring == "accuracy":
                    prediction = self.classifier.predict(feature_test)
                    score = accuracy_score(label_test, prediction, sample_weight=sample_weights_test)
                else:
                    raise ValueError(f"'{self.scoring}' method not defined.")

                scores.append(score)

            importances.append({
                "FeatureName": feature_name,
                "Mean": np.mean(scores),
                "StandardDeviation": np.std(scores, ddof=1) * len(scores) ** -0.5,
            })

        return pd.DataFrame(importances)

View More: Julia | Python

Orthogonal Features

Orthogonal features can reduce the dimensionality of your feature set and help in mitigating the substitution effects. This method also provides a safeguard against overfitting.

orthogonal_features.py

import pandas as pd
import numpy as np


def compute_eigenvectors(
        dot_product: np.ndarray,
        explained_variance_threshold: float
) -> pd.DataFrame:
    pass
    # See the source code for detailed implementations

def orthogonal_features(
        features: np.ndarray,
        variance_threshold: float = 0.95
) -> tuple:
    normalized_features = (features - features.mean(axis=0)) / features.std(axis=0)
    dot_product = normalized_features.T @ normalized_features
    eigen_dataframe = compute_eigenvectors(dot_product, variance_threshold)

    transformation_matrix = np.vstack(eigen_dataframe["EigenVector"].values).T

    orthogonal_features = normalized_features @ transformation_matrix

    return orthogonal_features, eigen_dataframe

View More: Julia | Python

How to Verify Your Features?

Weighted Kendall's Tau: Use this measure to compare the ranking of feature importance against their associated eigenvalues. A value closer to 1 indicates a more consistent relationship.
Research Methodologies:
- Per-instrument Feature Importance: Parallelize feature importance computation for each financial instrument. Aggregate the results.
- Features Stacking: Combine multiple datasets into one, normalizing features as necessary. The classifier will then determine the most important features across all instruments.

References

De Prado, M. L. (2018). Advances in financial machine learning. John Wiley & Sons.
De Prado, M. M. L. (2020). Machine learning for asset managers. Cambridge University Press.